Sonic Boom Lines
by Jeffrey Mattox, Madison, WI
Copyright 1995
 On maps and globes of the Earth, the locations of the
equator, the Arctic and Antarctic circles, and the tropics
of Cancer and Capricorn are clearly shown. These circles
indicate certain characteristics of the apparent journey
that the sun makes over the Earth's surface each year.
On maps and globes of the Earth, the locations of the
equator, the Arctic and Antarctic circles, and the tropics
of Cancer and Capricorn are clearly shown. These circles
indicate certain characteristics of the apparent journey
that the sun makes over the Earth's surface each year.
There are two other conjured circles on the Earth's
surface that few people know about. They are called "sonic
boom lines," and they indicate the latitudes where the
Earth's surface velocity is equal to the speed of sound.
Breaking the Barriers of Credulity
 You know that an aircraft produces a boom whenever it
accelerates above the speed of sound (approximately 760
miles per hour at 57 degrees F). The window-shattering sonic boom
that occurs when the aircraft "breaks the sound barrier" is
caused by an atmospheric shock wave that extends from the
aircraft to the ground. We rarely hear sonic booms today
because Federal Aviation Regulations (section 91.817)
prohibit all aircraft from flying at
supersonic speeds over inhabited areas.
You know that an aircraft produces a boom whenever it
accelerates above the speed of sound (approximately 760
miles per hour at 57 degrees F). The window-shattering sonic boom
that occurs when the aircraft "breaks the sound barrier" is
caused by an atmospheric shock wave that extends from the
aircraft to the ground. We rarely hear sonic booms today
because Federal Aviation Regulations (section 91.817)
prohibit all aircraft from flying at
supersonic speeds over inhabited areas.
However, despite federal regulations and public desires, the rotation of
the Earth causes many parts of the surface to spin at
velocities that exceed the speed of sound. Since the
circumference of the Earth is roughly 24,000 miles, the
surface speed at the equator due to the rotation of the
Earth is about 1,000 miles per hour (well above the speed of
sound).
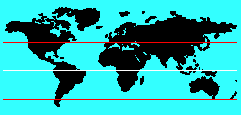 Using simple trigonometry, it is easy to compute the
latitude where the Earth's surface is moving at precisely
the speed of sound (computational details appear below).
At sea level and zero
degrees Celsius, that latitude is 44 degrees 21 minutes,
and a circle drawn around the Earth at that latitude is a
sonic boom line. Of course, there are two such lines; one
in the Northern Hemisphere, the other in the Southern
Hemisphere.
Using simple trigonometry, it is easy to compute the
latitude where the Earth's surface is moving at precisely
the speed of sound (computational details appear below).
At sea level and zero
degrees Celsius, that latitude is 44 degrees 21 minutes,
and a circle drawn around the Earth at that latitude is a
sonic boom line. Of course, there are two such lines; one
in the Northern Hemisphere, the other in the Southern
Hemisphere.
Unlike the equator and tropics, the exact locations of
the sonic boom lines vary according to local altitude and
air temperature. For example, using my altitude at Madison,
WI (978 feet above sea level) and average atmospheric
conditions (11.83 degrees C), the sonic boom line moves to 43 degrees 04'
55" north latitude. Although these effects are very small,
they are enough to make the exact locations of the boom
lines laborious to determine and in continuous flux. That
is why cartographers refuse to put these lines on their
maps.
Earth's Nether Regions
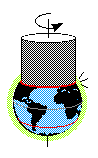 Technically, the sonic boom lines are the intersections
of an imaginary cylinder with the Earth's surface. The
center line of the cylinder is aligned with the Earth's
rotational axis and the surface of the cylinder (which
represents all points that are rotating at the speed of
sound) pierces the Earth's surface at the two sonic boom
latitudes. The two supersonic atmospheric regions that are
directly above the sonic boom lines at the Earth's surface
are called, curiously, the "nether regions." Those small
areas of the atmosphere dissipate the sonic boom shock waves
into outer space, thus preventing the shock waves from
causing a continuous, annoying boom to listeners on the
surface.
Technically, the sonic boom lines are the intersections
of an imaginary cylinder with the Earth's surface. The
center line of the cylinder is aligned with the Earth's
rotational axis and the surface of the cylinder (which
represents all points that are rotating at the speed of
sound) pierces the Earth's surface at the two sonic boom
latitudes. The two supersonic atmospheric regions that are
directly above the sonic boom lines at the Earth's surface
are called, curiously, the "nether regions." Those small
areas of the atmosphere dissipate the sonic boom shock waves
into outer space, thus preventing the shock waves from
causing a continuous, annoying boom to listeners on the
surface.
The Earth's motion around the sun and the sun's motion
through the cosmos do not affect the sonic boom phenomenon
nor produce one of their own. This is because sound waves
cannot travel through the vacuum of outer space.
A Minor Northern Nuisance
If you examine a map of the United States,
you will see
that the northern sonic boom line runs roughly from Boston,
MA, to Eugene, OR, and it goes through
Madison, WI. In
fact, the altitude and temperature-adjusted line (at 43 degrees 04'
55" north latitude) goes right though the center of my
house, piercing my font door and living room. Maybe this
explains the continuous ringing in my ears.
 Email me
[Genome Web site]
[Buddy Web site]
Email me
[Genome Web site]
[Buddy Web site]
This article was originally published in the Heurikon Horizon
(Heurikon Corporation's employee newsletter), February 1992.
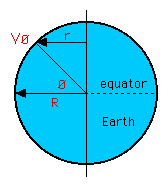 Computational Details:
Computational Details:
r = R * cos ø
Vø = (2 * pi * r) / t
Vø = (2 * pi * R * cos ø ) / (24 hours)
S = 44.856 * sqrt(273 + T) mph
where:
ø = degrees of latitude
R = radius of the Earth (3958.89 miles)
r = radius of rotation at latitude ø
t = period of Earth's rotation (24 hours)
Vø = velocity at latitude ø due to rotation
T = air temperature in degrees Celsius
S = speed of sound at temperature T
Solving for ø and setting Vø = S gives:
ø = arccos [ (24 hours * S) / (2 * pi * R) ]
ø = arccos [0.715] (at 0 degrees C)
ø = +/- 44.35 degrees
Updated: Oct 3, 2005
 On maps and globes of the Earth, the locations of the
equator, the Arctic and Antarctic circles, and the tropics
of Cancer and Capricorn are clearly shown. These circles
indicate certain characteristics of the apparent journey
that the sun makes over the Earth's surface each year.
On maps and globes of the Earth, the locations of the
equator, the Arctic and Antarctic circles, and the tropics
of Cancer and Capricorn are clearly shown. These circles
indicate certain characteristics of the apparent journey
that the sun makes over the Earth's surface each year. You know that an aircraft produces a boom whenever it
accelerates above the speed of sound (approximately 760
miles per hour at 57 degrees F). The window-shattering sonic boom
that occurs when the aircraft "breaks the sound barrier" is
caused by an atmospheric shock wave that extends from the
aircraft to the ground. We rarely hear sonic booms today
because Federal Aviation Regulations (section 91.817)
prohibit all aircraft from flying at
supersonic speeds over inhabited areas.
You know that an aircraft produces a boom whenever it
accelerates above the speed of sound (approximately 760
miles per hour at 57 degrees F). The window-shattering sonic boom
that occurs when the aircraft "breaks the sound barrier" is
caused by an atmospheric shock wave that extends from the
aircraft to the ground. We rarely hear sonic booms today
because Federal Aviation Regulations (section 91.817)
prohibit all aircraft from flying at
supersonic speeds over inhabited areas. Using simple trigonometry, it is easy to compute the
latitude where the Earth's surface is moving at precisely
the speed of sound (
Using simple trigonometry, it is easy to compute the
latitude where the Earth's surface is moving at precisely
the speed of sound ( Technically, the sonic boom lines are the intersections
of an imaginary cylinder with the Earth's surface. The
center line of the cylinder is aligned with the Earth's
rotational axis and the surface of the cylinder (which
represents all points that are rotating at the speed of
sound) pierces the Earth's surface at the two sonic boom
latitudes. The two supersonic atmospheric regions that are
directly above the sonic boom lines at the Earth's surface
are called, curiously, the "nether regions." Those small
areas of the atmosphere dissipate the sonic boom shock waves
into outer space, thus preventing the shock waves from
causing a continuous, annoying boom to listeners on the
surface.
Technically, the sonic boom lines are the intersections
of an imaginary cylinder with the Earth's surface. The
center line of the cylinder is aligned with the Earth's
rotational axis and the surface of the cylinder (which
represents all points that are rotating at the speed of
sound) pierces the Earth's surface at the two sonic boom
latitudes. The two supersonic atmospheric regions that are
directly above the sonic boom lines at the Earth's surface
are called, curiously, the "nether regions." Those small
areas of the atmosphere dissipate the sonic boom shock waves
into outer space, thus preventing the shock waves from
causing a continuous, annoying boom to listeners on the
surface.
 Computational Details:
Computational Details: